Probability distributions
We have explored the idea of probability, we can consider the concept of a probability distribution. In situations where the variable being studied is a random variable, then this can often be modelled by a probability distribution. Simply put, a probability distribution has two components – the collection of possible values that the variable can take, together with the probability that each of these values (or a subset of these values) occurs.
So, in stochastic modelling, a probability distribution is the equivalent of a function in deterministic modelling (in which there is no uncertainty). As we know, there are many different functions available for deterministic modelling and some of these are used more often than others e.g., linear functions, polynomial functions and exponential functions. Exactly the same situation prevails in stochastic modelling. Certain probability distributions are used more often than others. These include the Binomial distribution, the Poisson distribution, the uniform distribution, the normal distribution and the negative exponential distribution.
Discrete probability distribution
A discrete random variable assumes each of its values with a certain probability, i.e. each possible value of the random variable has an associated probability. Let X be a discrete random variable and let each value of the random variable have an associated probability, denoted p(x) = P(X = x), such that
| X: | X1 | X2 | . | . | . | Xn |
| p(x): | P1 | P2 | . | . | . | Pn |
The function p(x) is known as the probability distribution of the random variable X if the following conditions are satisfied-
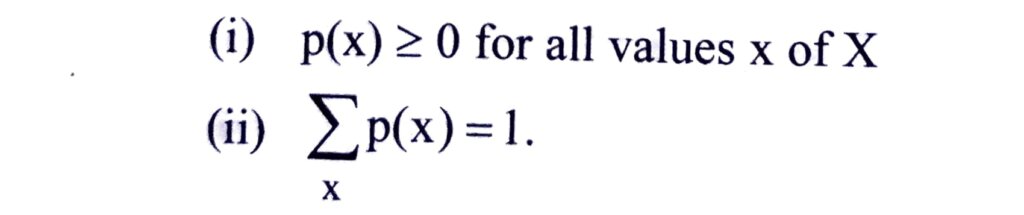
p(x) is also referred to as the probability function or probability mass function.
Write the expected value (or mean) and variance of a discrete probability distribution with an example.
Since the probability distribution for a random variable is a model for the relative frequency distribution of a population (think of organizing a very large number of observations of a discrete random variable into a relative frequency distribution – the probability distribution would closely approximate this), the analogous descriptive measures of the mean and variance are important concepts.
The expected value (or mean), denoted by E(X) or μ, of a discrete random variable X with probability function p(x) is defined as follows –
E(X) = ∑x p(x)
where the summation extends over all possible values x.
Note the similarity to the mean 1/n ∑fx (where n = ∑f) of a frequency distribution in which each value, x, is weighted by its frequency f. For a probability distribution, the probability p(x) replaces the observed frequency f.
The variance of a random variable X, denoted by Var(X) or σ², is defined as the expected value of the quantity (X-µ)2 where µ is the mean of X, i.e.
Var(X)=E[(X-μ)²]=Σ(x-µ)²p(x)
The standard deviation of X is the square root, σ, of the variance.
For Example – Consider an experiment that consists of tossing a fair coin three times, and let X equal the number of heads observed, describe the probability distribution of X, and hence determine E(X) and Var(X).
There are 8 possible outcomes here – HHH, HHT, HTH, THH, HTT, THT, TTH, TTT. This gives probability distribution as follows –
| X | Outcomes | Probability |
| 0 | TTT | 1/8 |
| 1 | HTT, THT, TTH | 3/8 |
| 2 | HHT, HTH, THH | 3/8 |
| 3 | HHH | 1/8 |
| Total Probability | 1.0 |
The expected value of X is-
E(X) = 0(1/8)+ 1(3/8) + 2(3/8) +3(1/8)
= 0 +3/8 + 6/8 + 3/8
= 12/8
= 1.5The variance of X is-
Var(X) =(0-1.5)2(1/8)+(1-1.5)2(3/8)+(2-1.5)2(3/8)
+(3-1.5)2(1/8)
= 2.25(1/8)+0.25(3/8)+0.25(3/8)+2.25(1/8)
= (2.25 + 0.75 +0.75 +2.25)/8
= 6/8
= 0.75There is an alternative way of computing Var(X). It can be shown that – Var(X) = ∑x².p(x) – [∑x p(x)]2. Using this result we have the table 1.3.
| X | P(x) | XP(x) | X2 p(x) |
| 0 | 1/8 | 0 | 0 |
| 1 | 3/8 | 3/8 | 3/8 |
| 2 | 3/8 | 6/8 | 12/8 |
| 3 | 1/8 | 3/8 | 9/8 |
| Total | 1.0 | 1.5 | 3.0 |
Var(X) = 3.0 – 1.52 =3.0-2.25 = 0.75.








