What do you mean by probability density function?
In a discrete random variable, probabilities are associated with particular individual values of the random variable, and the sum of all probabilities is one. For a continuous random variable X, we do not have a formula that gives the probability of any particular value of X. The probability that a continuous random variable X assumes a specific value x is taken to be zero,
For a continuous random variable, we deal with probabilities of intervals rather than probabilities of particular individual values.
The probability distribution of continuous random variable X is characterized by a function f(x) known as the probability density function. This function is not the same as the probability function in the discrete case. Since the probability that X is equal to a specific value is zero, the probability density function does not represent the probability that X=x. Rather, it provides the means by which the probability of an interval can be determined.
The function f(x) whose graph is the limiting curve is the probability density function of the continuous random variable X, provided that the vertical scale is chosen in such a way that the total area under the curve is one.
Let X be a continuous random variable. The function f(x) is said to be a probability density function, if
(i) f(x) ≥0, for every value of x
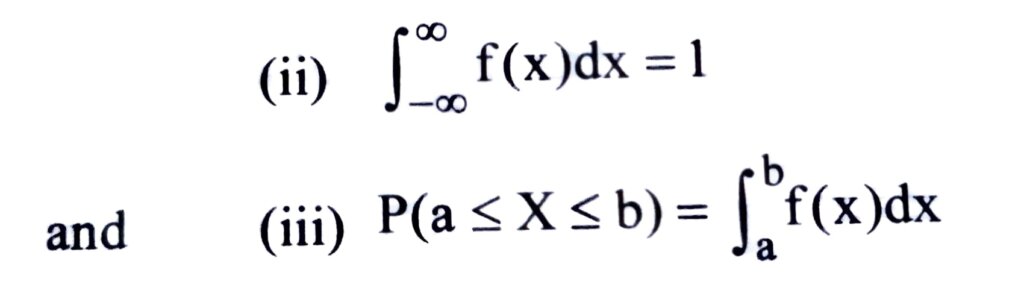
for any a and b.
The third condition indicates how the function is used- The probability that X will assume some value in the interval [a, b]= the area under the curve between x-a and x-b. This is the shaded area as shown in Fig. 1.3.
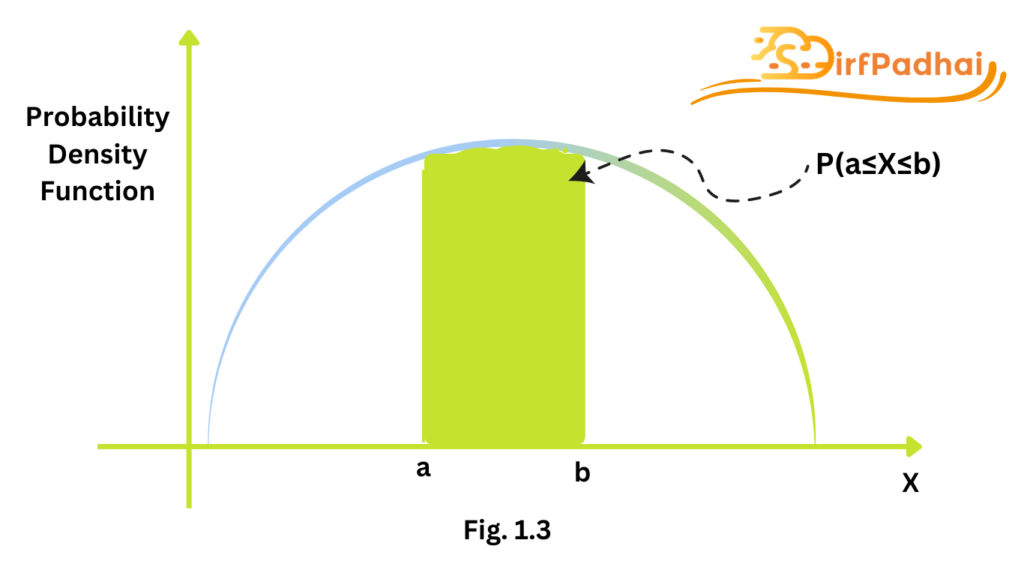
In general, the exact evaluation of areas requires us to use the probability density function f(x) and integral calculus. These calculations are time-consuming and not straightforward. However, probability values can be obtained from statistical tables (just as for discrete probability distributions).