Support Vector Machine(SVM)

Support Vector Machine

Support vector machines are supervised learning models with associated learning algorithms that analyze data after which they are used for classification. Classification refers to which images are related to which class or data set or set of categories. In machine learning classification is considered an instance of supervised learning which refers to the task of inferring a function from labelled training data. Training data in image retrieval process can be correctly identified images that are put in a particular class. Where each class belongs to a different category of images. In the SVM training algorithms model is build in which the new examples are assigned to one category class or other. In this model representation of examples in categories is done with clear gaps that are as vast as possible.

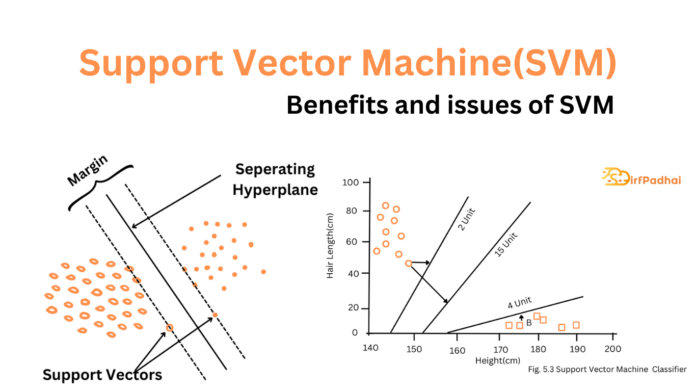
The main idea of SVM is to construct the hyperplane in a high-dimensional space that can be used for classification. Hyperplane refers to a subspace one dimension less than its ambient space. If there is 3-dimensional space then its hyperplane is the 2-dimensional plane. By hyperplane a good separation is achieved that has the largest distance to the nearest training data point of any class. The separation between the hyperplane and the closet data point is called the margin of separation. So more the margin of separation less be the generalization error of the classifier.

The main objective of the SVM machine is to find a particular hyper-plane for which the margin of separation is very high or which can be controlled to be maximized when this condition is met or we can under these circumstances, the decision plane which we take to differentiate between two classes, and then it is called an as optimal hyperplane. The support vectors play an important role in the operation of this class of learning machines as we can define support vectors as the elements of the training data set that would change the position of the dividing hyper-plane in the SVM training algorithm if they are removed. As maximum-margin hyper-plane and margins for an SVM trained with samples from two classes and these samples on the margin are called support vectors or we can say that these are data point that lies closest to the decision surface.

Discuss the key idea of the support vector machines (SVMs).

The most widely used state-of-the-art machine learning technique is Support Vector Machine (SVM). It is mainly used for classification. SVM works on the principle of margin calculation. It basically, draws margins between the classes. The margins are drawn in such a fashion that the distance between the margin and the classes is maximum and hence, minimizing the classification error. The working of SVM is given in Fig. 5.1.

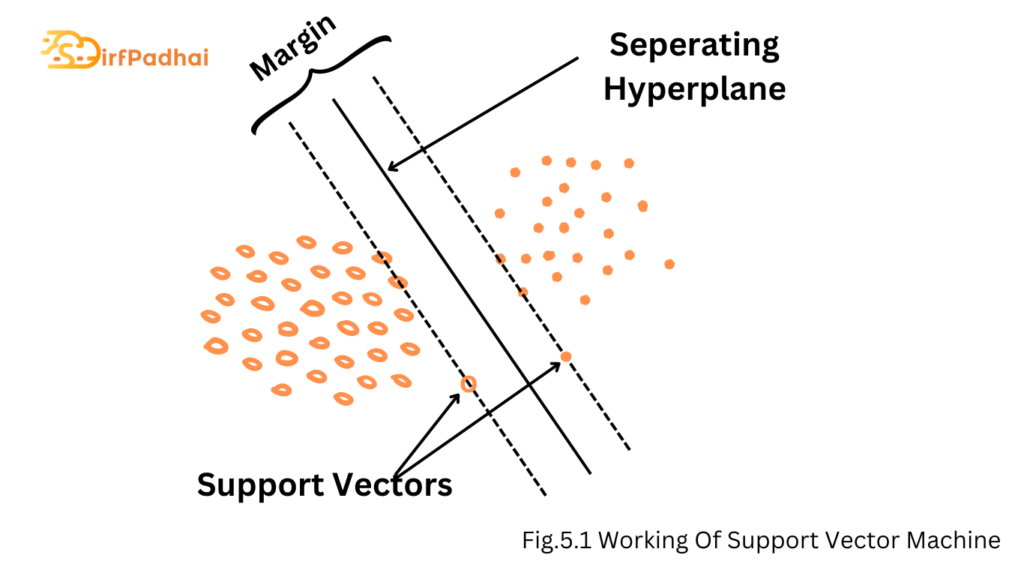
Input – S, λ, T, K

Initialize – Choose w₁ s.t. ∥w₁∥≤1/√λ

For t = 1, 2, ……., T

Choose A_t ⊆ S, where |A_t |=k

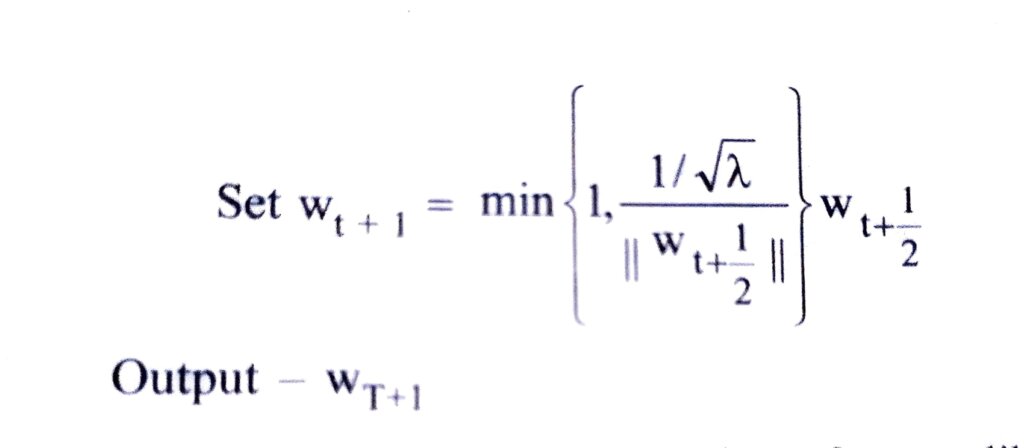
For Example- If we only had two features like the height and hair length of an individual, we would first plot these two variables in two-dimensional space where each point has two co-ordinates, these co-ordinates are known as support vectors.

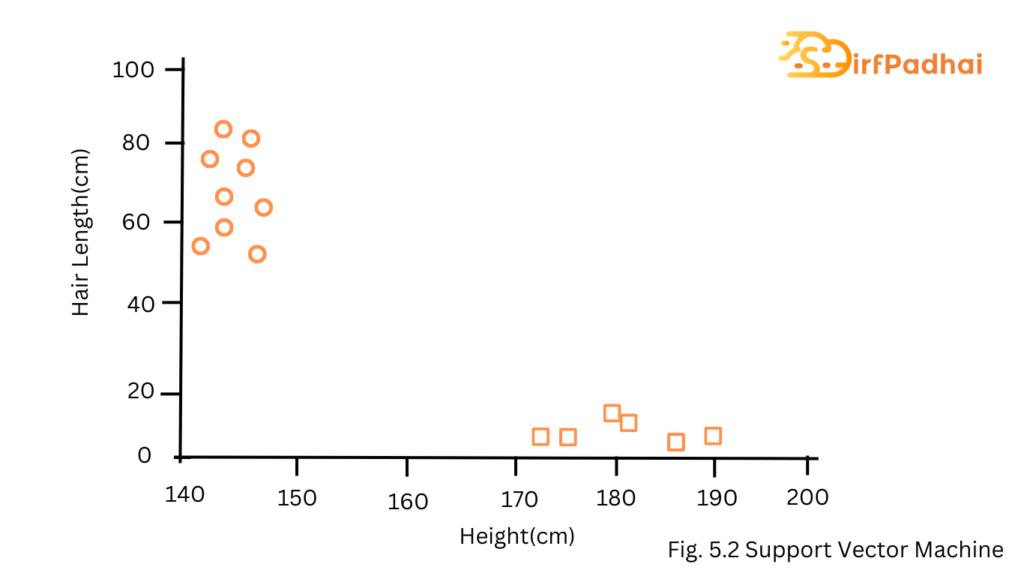
Now, we will find some lines that split the data between the two differently classified groups of data. This will be the line such that the distances from the closest point in each of the two groups will be farthest away.

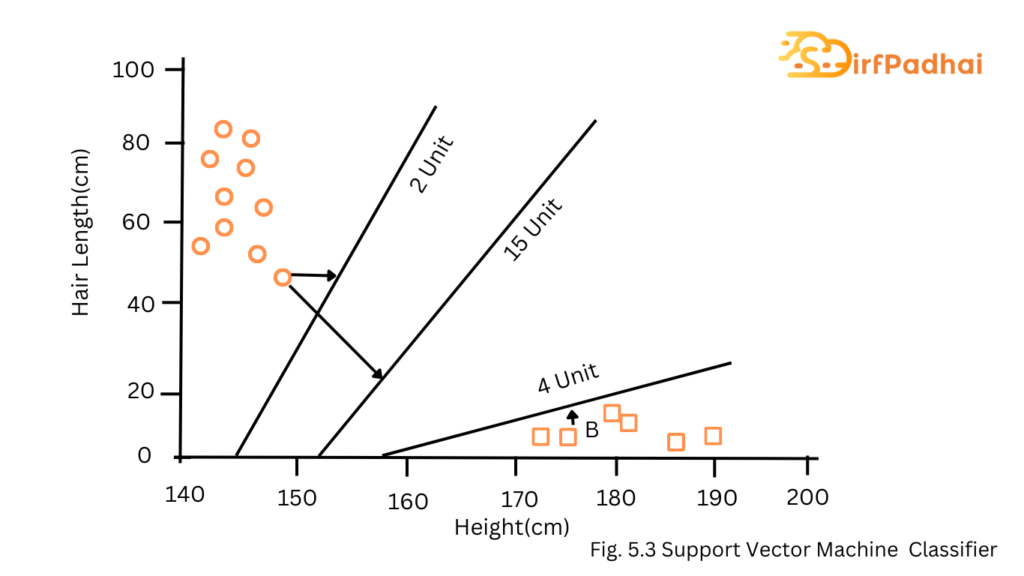
In the example shown above, the line which splits the data into two differently classified groups is the black line, since the two closest points are the farthest apart from the line. This line can be considered as a classifier.

Then, depending on where the testing data lands on either side of the line, that is what class we can classify the new data as.

Think of this algorithm as playing JezzBall in n-dimensional space. The tweaks in the game are –

(1) We can draw lines/planes at any angle (rather than just horizontal or vertical as in classic games).

(2) The objective of the game is to segregate balls of different colors in different rooms.

(3) And the balls are not moving.

Write down the benefits and issues of SVM.

Benefits –

There are a number of benefits to using SVM as follows-

(1) It is effective in high-dimensional space.

(2) Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.

(3) It is versatile because holds different kernel functions that can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels.

Issues –

The issue that is to be faced in SVM is the hyperplane. constructed by SVM is dependent on only a fraction of training samples called support vectors (SVS) which recline close to the resulting border as well as removing some training samples that are not applicable to support vectors may possibly have no effect on building the appropriate decision function.

Strengths of SVM

• SVM can be used for both classification and regression.
• It is robust, i.e. not much impacted by data with noise or outliers.
• The prediction results using this model are very promising.

Weakness of SVM

• SVM is applicable only for binary classification, i.e. when there are only two classes in the problem domain.
• The SVM model is very complex- almost like a black box when it deals with a high-dimensional data set. Hence, it is very difficult and close to impossible to understand the model in such cases.
• It is slow for a large dataset. i.e. a data set with either a large number of features or a large number of instances.
• It is quite memory-intensive.

Application of SVM

SVM is most effective when it is used for binary classification, i.e. for solving a machine-learning problem with two classes. One common problem on which SVM can be applied is in the field of bioinformatics more specifically, in detecting cancer and other genetic disorders. It can also be used in detecting the image of a face by binary classification of images into face and non-face components. More Sach applications can be described.